Bienvenido, nuevo curso

Muy buenas y bienvenidos a mi nuevo blog sobre las matemáticas académicas.
Son una alumna a la que le gustan las matemáticas pero le cuesta mucho realizar los ejercicios porque no entiende nada, y como soy tímida, no me atrevo a preguntar mis dudas delante de toda la clase.
Espero que este curso me vaya muy bien, tengo ganas de aprobar y poder graduarme.
Siempre pensaré que las matemáticas son difíciles.

 

 

María Gaetana Agnesi

María Gaetana Agnesi (16/05/1718 - 09/01/1799)

Lingüista, matemática y filósofa italiana

Nació el 16 de mayo de 1718 en Milán.
Falleció el 9 de enero de 1799 en Milán.
Desde niña habló francés, latín, griego y hebreo entre otras lenguas.
A los nueve años escribe un discurso defendiendo la educación de las mujeres. Quiso recluirse en un convento pero su padre se negó.

Reemplazó a su padre en la cátedra de matemáticas de la Universidad de Bolonia cuando éste estuvo enfermo siendo la primera mujer en ocupar una cátedra de matemáticas.

Dedicó su vida al estudio de las matemáticas y al cuidado de sus veinte hermanos.

Su trabajo más importante fue "Instituzioni Analithe" (Instituciones Analíticas), basado en cálculo diferencial e integral y publicado en 1748.

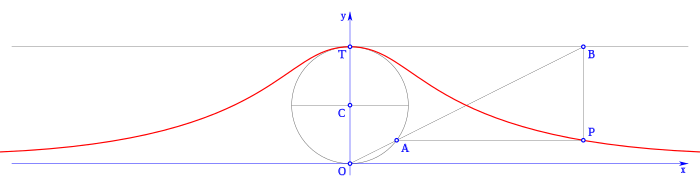
Fue conocida también como La Bruja de Agnesi por una mala traducción de su libro de la palabra versoria (nombre latino de la curva de una función), por versiera otra palabra que significa abuela del diablo o bruja, de ahí viene el nombre adoptado también por la curva, La Bruja de Agnesi.

 

ECUACIONES

Los sistemas de ecuaciones son un conjunto de dos o más ecuaciones con varias incógnitas. Hay tres métodos para resolver los sistemas:

1. Método de sustitución 
Consiste en aislar en una ecuación una de las dos incógnitas para sustituirla en la otra ecuación.

2. Método de reducción 
Consiste en sumar o restar las ecuaciones del sistema para eliminar una de las incógnitas.

3. Método de igualación
Consiste en aislar una incógnita en las dos ecuaciones para igualarlas.

TRIGONOMETRÍA

La trigonometría es la rama de las matemáticas que estudia la relación entre los lados y ángulos de los triángulos. Se ocupa de las funciones asociadas a los ángulos, denominadas funciones trigonométricas: seno, coseno, tangente...


Las razones trigonométricas de un angulo α son las razones obtenidas entre los tres lasdos de un triángulo rectángulo. Es decir, la comparación por su cociente de sus tres lados a, b y c.

FUNCIONES

Funciones

Una función lineal es una función polinómica de primer grado, en una gráfica se representa como una recta. Se escribe: f(x) = mx + b.

Una función cuadrática es una función polinómica de segundo grado que se escribe: f(x) = ax2 + bx + c

Binomio de Newton

El cuadrado de una suma (a + b)² o el cuadrado de una resta (a - b)² son sólo los casos más sencillos cuando elevamos un binomio a una potencia. Para estos casos, son conocidas las fórmulas "el cuadrado del primero más (o menos) el doble del primero por el segundo más el cuadrado del segundo", es decir:
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
Si generalizamos esto para cualquier exponente n, tenemos lo que se conoce como "Binomio de Newton". Según esta fórmula, los coeficientes del desarrollo de (a + b)ⁿ son los números combinatorios  mientras que los términos van disminuyendo el grado de a de uno en uno y aumentando el de b de uno en uno (de forma que la suma de los exponentes siempre es n), con lo que obtenemos:



Triángulo de Pascal o Tartaglia

Pascal ideó una manera sencilla de calcular números combinatorios

Se construye de la siguiente manera:

-En el vértice se coloca un 1
-Cada fila empieza y acaba en 1
-Los otros números de la fila son siempre la suma de los dos que tienen justo encima

Polinomios

Llamamos polinomio a aquella expresión constituida por un conjunto finito de variables (no determinadas o desconocidas) y constantes (números fijos llamados coeficientes), utilizando únicamente las operaciones aritméticas de suma, resta y multiplicación, así como exponentes enteros positivos. Es decir, que un polinomio es una combinación lineal de productos de potencias enteras de una o varias indeterminadas.

El grado de un monomio se define como el exponente de su variable. El grado de un polinomio es el del monomio de mayor grado.

Os dejo estos ejemplos: 

 P(x) = 2, polinomio de grado cero (el polinomio solo consta del término independiente).

 P(x) = 3x + 2, polinomio de grado uno.

 P(x) = 6x² + 2x, polinomio de grado dos

 P(x) = 2x³+ 3x + 5, polinomio de grado tres.

 P(x) = 4x⁴+ 6x + 2, polinomio de grado cuatro

 P(x) = 2x⁵+ 3x + 1, polinomio de grado cinco.

Polinomio ceroEditar

Es el 0, tiene grado -1. Actúa de elemento neutro aditivo: p(x) +0= p(x), para cualquier p(x).

Polinomio de grado ceroEditar

Es aquel que no lleva la indeterminada. Son los elementos no nulos de conjuntos numéricos correspondientes.